Huffman coding
Motivation
Compression (a short video clip on text compression); unlike ASCII or Unicode encoding, which use the name number of bits to encode each character, a Huffman code uses different numbers of bits to encode the letters: more bits for rare letters, and fewer bits for common letters.Compression can be achieved further at words level and so on.
Image compression/music compression/text compression/genomic sequence compression (see a paper about genome compression)
Definition
Huffman coding assigns codes to characters such that the length of the code depends on the relative frequency or weight of the corresponding character. Huffman codes are of variable-length, and prefix-free (no code is prefix of any other). Any prefix-free binary code can be visualized as a binary tree with the encoded characters stored at the leaves.
A Huffman coding tree or Huffman tree is a full binary tree in which each leaf of the tree corresponds to a letter in the given alphabet.
Define: the weighted path length of a leaf to be its weight times its depth.
The Huffman tree is the binary tree with minimum external path weight, i.e., the one with the minimum sum of weighted path lengths for the given set of leaves.
So the goal is to build a tree with the minimum external path weight.
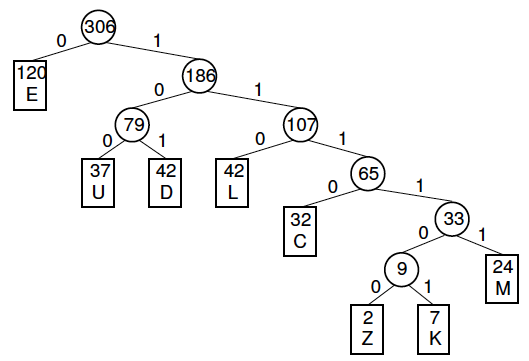
See an example below:
Letter freqency table
| Letter | Z | K | M | C | U | D | L | E |
| Frequency | 2 | 7 | 24 | 32 | 37 | 42 | 42 | 120 |
Huffman code
| Letter | Freq | Code | Bits |
| E | 120 | 0 | 1 |
| D | 42 | 101 | 3 |
| L | 42 | 110 | 3 |
| U | 37 | 100 | 3 |
| C | 32 | 1110 | 4 |
| M | 24 | 11111 | 5 |
| K | 7 | 111101 | 6 |
| Z | 2 | 111100 | 6 |
Three problems
- Problem 1: Huffman tree building
- Problem 2: Encoding
- Problem 3: Decoding
Problem 2: Encoding
Encoding a string can be done by replacing each letter in the string with its binary code (the Huffman code).
Examples:
DEED 10100101 (8 bits)
MUCK 111111001110111101 (18 bits)
Problem 3: Decoding
Decoding an encoded string can be done by looking at the bits in the coded string from left to right until a letter decoded.
10100101 -> DEED
The Huffman codes are prefix free--a set of codes is said to meet the prefix property if no code in the set is the prefix of another. The prefix property guarantees that there will be no ambiguity in how a bit string is decoded.
Problem 1: Huffman tree building
A simple algorithm (buildHuff):
- Prepare a collection of n initial Huffman trees, each of which is a single leaf node.
Put the n trees onto a priority queue organized by weight (frequency).
- Remove the first two trees (the ones with lowest weight). Join these two trees to create a new tree whose root has the two trees as children, and whose weight is the sum of the weights of the two children trees.
- Put this new tree into the priority queue.
- Repeat steps 2-3 until all of the partial Huffman trees have been combined into one.
It's a greedy* algorithm: at each iteration, the algorithm makes a "greedy" decision to merge the two subtrees with least weight. Does it give the desired result?
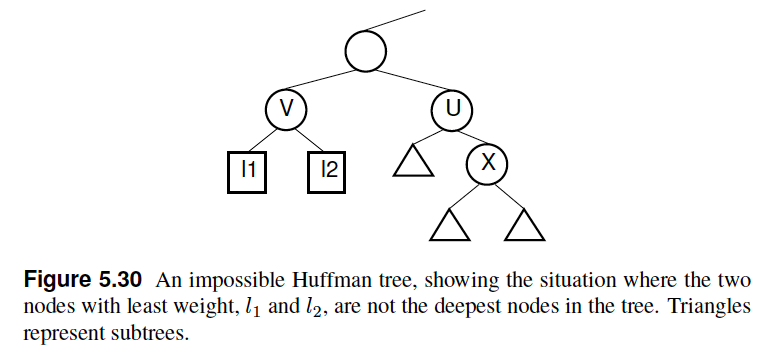
- Lemma: Let $x$ and $y$ be the two least frequent characters. There is an optimal code tree in which $x$ and $y$ are siblings whose depth is at least as any other leaf nodes in the tree.
Proof: Call the two letters with least frequency $l_1$ and $l_2$. They must be siblings because buildHuff selects them in the first step of the construction process. Assume that $l_1$ and $l_2$ are not the deepest nodes in the tree. In this case, the Huffman tree must either look as shown in Figure 5.30 (Shatter), or in some sense be symmetrical to this. For this situation to occur, the parent of $l_1$ and $l_2$, labeled $V$, must have greater weight than the node labeled $X$. Otherwise, function buildHuff would have selected node $V$ in place of node $X$ as the child of node $U$. However, this is impossible because $l_1$ and $l_2$ are the letters with least frequency.
- Theorem: The greedy algorithm builds the Huffman tree with the minimum external path weight for a given set of letters (i.e., Huffman codes are optimal prefix-free binary codes)
Proof: The proof is by induction on $n$, the number of letters.- Base Case: For n = 2, the Huffman tree must have the minimum external path weight, because there are only two possible trees, each with identical weighted path lengths for the two leaves.
- Induction Hypothesis: Assume that any tree created by buildHuff that contains $n-1$ leaves has minimum external path length.
- Induction Step: Given a Huffman tree T built by buildHuff with $n$ leaves ($n \geq 2$), suppose that $w_1 \leq w_2 \dots \leq w_n$, where $w_1$ to $w_n$ are the weights of the letters. Call $V$ the parent of the letters with frequencies $w_1$ and $w_2$. From the lemma, we know that the leaf nodes containing the letters with frequencies $w_1$ and $w_2$ are as deep as any nodes in T. Call T' the Huffman tree that is identical to T except that node $V$ is replaced with a leaf node $V'$ whose weight is $w_1 + w_2$. By the induction hypothesis, T' has minimum external path length. Returning the children to $V'$ restores tree T, which must also have minimum external path length.
Implementation
See an implementation at github (HuffTree.java) (note getCode function is to be implemented by students)
For bored: compression algorithms; lossless vs lossy
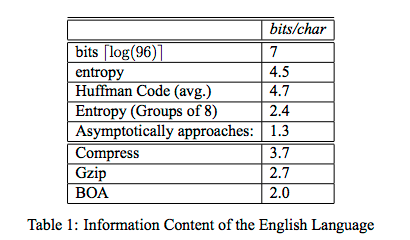
(image taken from https://www.cs.cmu.edu/~guyb/realworld/compression.pdf)